Çözümleyici Çizelge İle Önermenin Tutarlılığını Denetleme
Herhangi bir önermenin tutarlılığı denetlenirken, çözümleme kurallarının aynısı uygulanır.
Çözümleme sonunda, yolların ucunda en az bir açık yol varsa önerme tutarlıdır. Çünkü, bu durum önermenin en az bir tane doğru değerine sahip olduğunu gösterir. Hiç açık yol yoksa önerme tutarsız demektir.
Konu Başlıkları
ÖRNEKLER
Örnek 1
(~p V q) Λ (p Λ q) önermesinin tutarlılığını denetleyelim.
Önermenin ana eklemi tümel evetleme ( Λ ) eklemidir. Bu nedenle çözümlemeye alt alta yazma kuralı uygulanarak başlanır ve aşağıdaki yol izlenir:
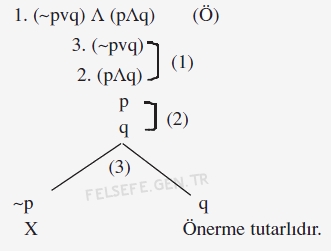
Çözümlemeye önermenin sağ tarafına adım numarasını, sol tarafına başlangıç önermesi olduğunu belirten (Ö) harfini koyarak başladık.
Tümel evetleme kuralına göre bileşenleri alt alta yazdık.
Görüldüğü gibi, elde edilen iki önermeden biri tümel evetleme diğeri tikel evetleme önermesidir. İşlem sırasına göre ilk önce tümel evetleme yapılacağı için, kural gereği tümel evetleme önermesini (2) çözümledik.
Çelişki ortaya çıkmadığı için tikel evetleme önermesini (3) çözümledik. Böylece işlem tamamlandı.
Ortaya çıkan iki yoldan birisinde p ve ~p önermeleri çelişti. Bu nedenle o yolu (X) işaretiyle kapattık. Diğer yol açık olduğu için çözümlediğimiz önerme tutarlı çıktı.
Örnek 2
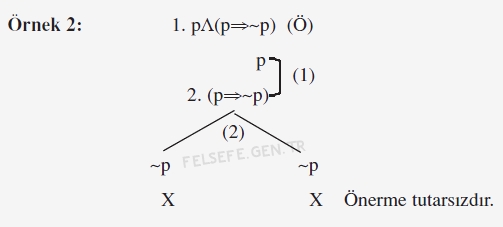
Yukarıdaki örnekte, verilen önermenin ana eklemi tümel evetleme olduğu için birinci adımda alt alta yazarak çözümledik.
İkinci adımda, koşul önermesini çözümleme kuralına göre (p => q ≡ ~p v q denkliği gereği) çatal açarak çözümledik.
Her iki yolda çıkan ~p önermesi yukarıdaki p önermesi ile çeliştiği için önerme tutarsızdır.
Peki önermeler birden fazla ise tutarlılık nasıl denetlenir?
BİRDEN FAZLA ÖNERMENİN TUTARLILIĞININ DENETLENMESİ
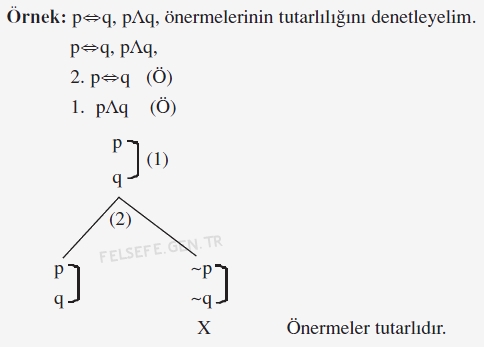
Birden fazla önerme denetlenirken, kaç tane önerme verilmişse alt alta yazılır ve çözümleme kuralları uygulanır.
Hazırlayan: Sosyolog Ömer YILDIRIM
Kaynak: Ömer YILDIRIM’ın Kişisel Ders Notları. Atatürk Üniversitesi Sosyoloji Bölümü 3. Sınıf “Klasik Mantık” ve “Modern Mantık” Dersleri Ders Notları (Ömer YILDIRIM)

